Performance of package

Graph of compute time as function of dimension

We can use the functions compare_eta_comptime_across_nvars() and plot_eta_comptime() to investigate computation time of the algorithm for varying dimension of the parameter vector $\beta$. This can also be used to investigate computation time for different sample methods, different tuning parameters, or whatever the user might be interested in.

The basic usage of the function can be used to investigate the computational gain for high dimensions of the CGGibbs sampler compared to the naive approach of doing $d$ computation for each coordinate update. For this purpose, the function call is:

res <- compare_eta_comptime_across_nvars(
  n_vars = c(2, seq(from = 50, to = 500, by = 50)),
  n_samples = 1,
  burnin = 0,
  w = 0.5)

The results can be plotted by simply calling

plot_eta_comptime(res)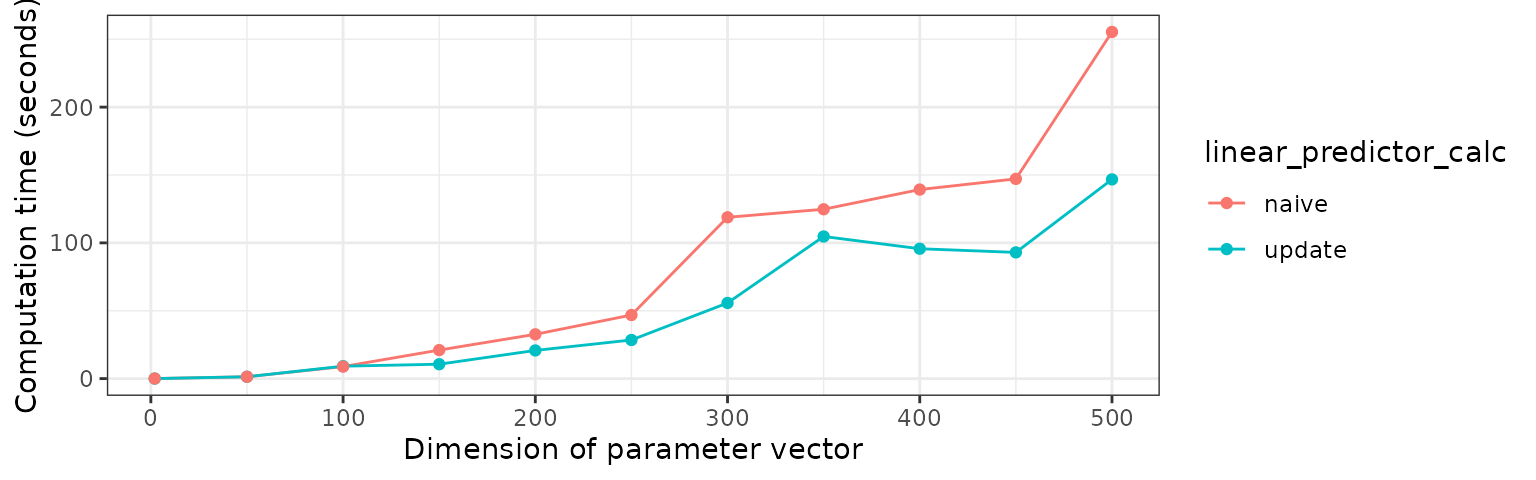

Runtime across dimensions for different sampling methods

The user can easily just iterate the function across different sampling procedures or tuning parameters for a single sample procedure, bind the results, and then use the facet_by argument in plot_eta_comptime().

An example of this could look like: > We won’t run this code for this vignette to reduce rendering time, but it provides an idea to what is possible using the functionalities.

ws <- c(0.5, 5, 20, 100)
res <- lapply(ws, function(w) {
  compare_eta_comptime_across_nvars(
    w = w,
    n_vars = c(2, seq(from = 10, to = 50, by = 10)),
    n_samples = 50,
    burnin = 1,
    parallelise = TRUE)
}) %>% 
  dplyr::bind_rows()

plot_eta_comptime(res, facet_by = "w")